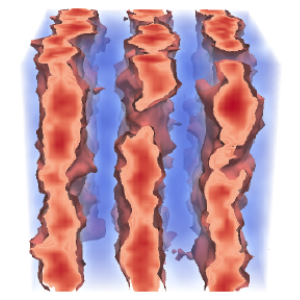
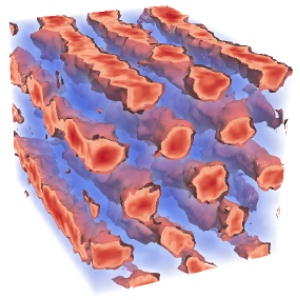
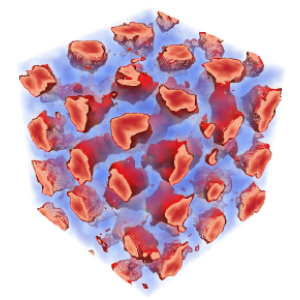
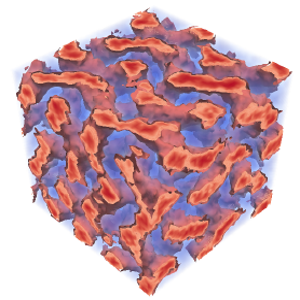
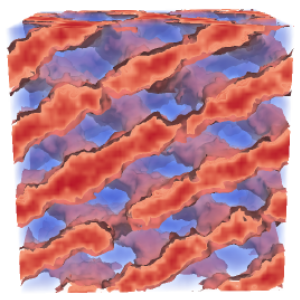
Fluctuation stabilization of the Fddd network phase in diblock, triblock, and starblock copolymer melts.
Self-consistent field theory has demonstrated that the homologous series of \((AB)_{M}\) starblock copolymers are promising architectures for the complex network Fddd phase. Nevertheless, it remains to be seen if the level of segregation will be sufficient to survive the fluctuations inevitably present in experiments. Here, we study the effect of fluctuations using field-theoretic simulations, which are uniquely capable of evaluating order-order phase transitions. This facilitates the calculation of complete fluctuation-corrected diagrams for the diblock \((M=1)\), symmetric triblock \((M=2)\), and nine-arm starblock \((M=9)\) architectures. Although fluctuations disorder the Fddd phase at weak segregations, they also stabilize the Fddd phase with respect to its ordered neighbors, which extends the Fddd region to higher segregation. Our results provide strong evidence that Fddd will remain stable in experiments on the side of the phase diagram where the outer \(A\) blocks of the star form the network domain. However, it is doubtful that Fddd will survive fluctuations on the other side where they form the matrix domain.
Fluctuation-corrected phase diagrams for diblock copolymer melts.
New developments in field-theoretic simulations (FTSs) are used to evaluate fluctuation corrections to the self-consistent field theory of diblock copolymer melts. Conventional simulations have been limited to the order-disorder transition (ODT), whereas FTSs allow us to evaluate complete phase diagrams for a series of invariant polymerization indices. The fluctuations stabilize the disordered phase, which shifts the ODT to higher segregation. Furthermore, they stabilize the network phases at the expense of the lamellar phase, which accounts for the presence of the Fddd phase in experiments. We hypothesize that this is due to an undulation entropy that favors curved interfaces.
Accounting for the ultraviolet divergence in field-theoretic simulations of block copolymer melts.
This study examines the ultraviolet (UV) divergence in field-theoretic simulations (FTSs) of block copolymer melts, which causes an unphysical dependence on the grid resolution, \(\Delta\), used to represent the fields. Our FTSs use the discrete Gaussian-chain model and a partial saddle-point approximation to enforce incompressibility. Previous work has demonstrated that the UV divergence can be accounted for by defining an effective interaction parameter, \( \chi = z_{\infty}\chi_{b} + c_{2}\chi_{b}^{2} + c_{3}\chi_{b}^{3} + \ldots \), in terms of the bare interaction parameter, \(\chi_{b}\), used in the FTSs, where the coefficients of the expansion are determined by a Morse calibration. However, the need to use different grid resolutions for different ordered phases generally restricts the calibration to the linear approximation, \(\chi \approx z_{\infty}\chi_{b}\), and prevents the calculation of order-order transitions. Here, we resolve these two issues by showing how the nonlinear calibration can be translated between different grids and how the UV divergence can be removed from free energy calculations. By doing so, we confirm previous observations from particle-based simulations. In particular, we show that the free energy closely matches self-consistent field theory (SCFT) predictions, even in the region where fluctuations disorder the periodic morphologies, and similarly, the periods of the ordered phases match SCFT predictions, provided the SCFT is evaluated with the nonlinear \(\chi\).
Well-tempered metadynamics applied to field-theoretic simulations of diblock copolymer melts.
Well-tempered metadynamics (WTMD) is applied to field-theoretic simulations (FTS) to locate the order-disorder transition (ODT) in incompressible melts of diblock copolymer with an invariant polymerization index of \(\bar{N} = 10^{4}\). The polymers are modeled as discrete Gaussian chains with \(N = 90\) monomers, and the incompressibility is treated by a partial saddle-point approximation. Our implementation of WTMD proves effective at locating the ODT of the lamellar and cylindrical regions, but it has difficulty with that of the spherical and gyroid regions. In the latter two cases, our choice of order parameter cannot sufficiently distinguish the ordered and disordered states because of the similarity in microstructures. The gyroid phase has the added complication that it competes with a number of other morphologies, and thus, it might be beneficial to extend the WTMD to multiple order parameters. Nevertheless, when the method works, the ODT can be located with impressive accuracy (e.g., \(\Delta \chi N \sim 0.01\)).
Field-theoretic simulations for block copolymer melts using the partial saddle-point approximation.
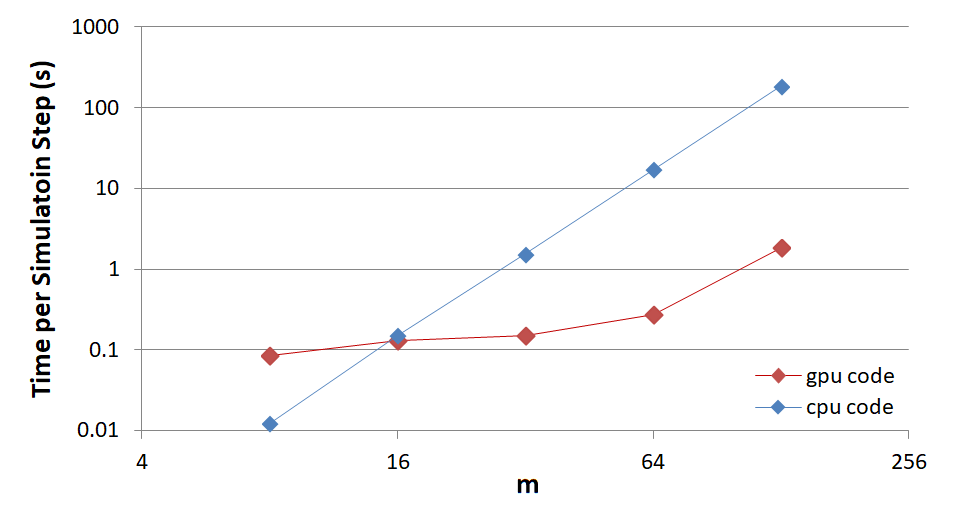
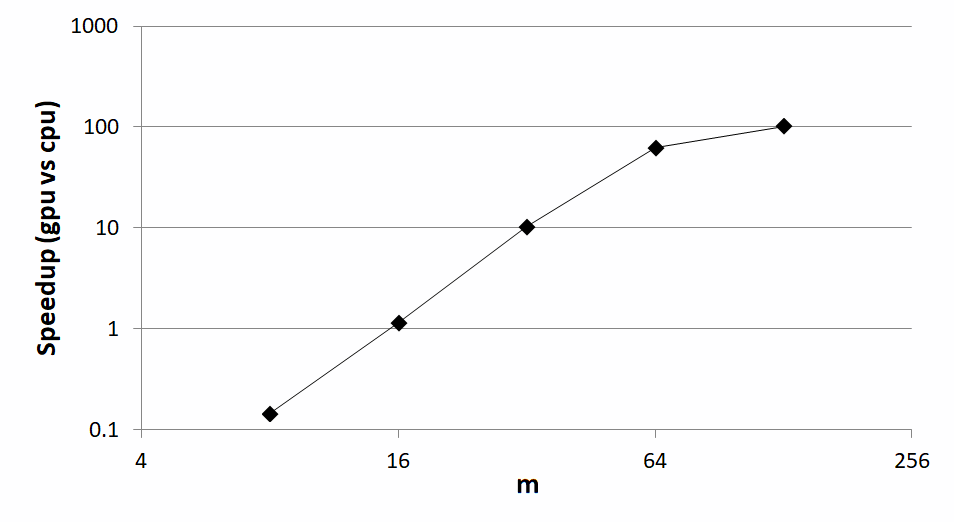
Field-theoretic simulations (FTS) provide an efficient technique for investigating fluctuation effects in block copolymer melts with numerous advantages over traditional particle-based simulations. For systems involving two components (i.e., \(A\) and \(B\)), the field-based Hamiltonian, \(H_{f}[W_{-}, W_{+}]\), depends on a composition field, \(W_{-}(r)\), that controls the segregation of the unlike components and a pressure field, \(W_{+}(r)\), that enforces incompressibility. This review introduces researchers to a promising variant of FTS, in which \(W_{-}(r)\) fluctuates while \(W_{+}(r)\) tracks its mean-field value. The method is described in detail for melts of \(AB\) diblock copolymer, covering its theoretical foundation through to its numerical implementation. We then illustrate its application for neat \(AB\) diblock copolymer melts, as well as ternary blends of \(AB\) diblock copolymer with its \(A-\) and \(B-\)type parent homopolymers. The review concludes by discussing the future outlook. To help researchers adopt the method, open-source code is provided that can be run on either central processing units (CPUs) or graphics processing units (GPUs).
Fluctuation correction for the order-disorder transition of diblock polymer melts.
The order-disorder transition (ODT) of diblock copolymer melts is evaluated for an invariant polymerization index of \(\bar{N}=10^{4}\), using field-theoretic simulations (FTS) supplemented by a partial saddle-point approximation for incompressibility. For computational efficiency, the FTS are performed using the discrete Gaussian-chain model, and results are then mapped onto the continuous model using a linear approximation for the Flory-Huggins \(\chi\) parameter. Particular attention is paid to the complex phase window. Results are found to be consistent with the well-established understanding that the gyroid phase extends down to the ODT. Furthermore, our simulations are the first to predict that the Fddd phase survives fluctuation effects, consistent with experiments.
Computationally efficient field-theoretic simulations for block copolymer melts.
Field-theoretic simulations (FTS) provide fluctuation corrections to self-consistent field theory (SCFT) by simulating its field-theoretic Hamiltonian rather than applying the saddle-point approximation. Although FTS work well for ultrahigh molecular weights, they have struggled with experimentally relevant values. Here, we consider FTS for two-component (i.e., AB-type) melts, where the composition field fluctuates but the saddle-point approximation is still applied to the pressure field that enforces incompressibility. This results in real-valued fields, thereby allowing for conventional simulation methods. We discover that Langevin simulations are 1-2 orders of magnitude faster than previous Monte Carlo simulations, which permits us to accurately calculate the order-disorder transition of symmetric diblock copolymer melts at realistic molecular weights. This remarkable speedup will, likewise, facilitate FTS for more complicated block copolymer systems, which might otherwise be unfeasible with traditional particle-based simulations.
Calibration of the Flory-Huggins interaction parameter in field-theoretic simulations.
Field-theoretic simulations (FTS) offer a versatile method of dealing with complicated block copolymer systems, but unfortunately they struggle to cope with the level of fluctuations typical of experiments. Although the main obstacle, an ultraviolet divergence, can be removed by renormalizing the Flory-Huggins \(\chi\) parameter, this only works for unrealistically large invariant polymerization indexes, \(\bar{N}\). Here, we circumvent the problem by applying the Morse calibration, where a nonlinear relationship between the bare \(\chi_{b}\) used in FTS and the effective \(\chi\) corresponding to the standard Gaussian-chain model is obtained by matching the disordered-state structure function, \(S(k)\), of symmetric diblock copolymers to renormalized one-loop predictions. This calibration brings the order-disorder transition obtained from FTS into agreement with the universal results of particle-based simulations for values of \(\bar{N}\) characteristic of the experiment. In the limit of weak interactions, the calibration reduces to a linear approximation, \(\chi \approx z_{\infty}\chi_{b}\), consistent with the previous renormalization of \(\chi\) for large \(\bar{N}\).