Diblock Copolymers (DBCs)
A diblock copolymer consists of an A-block of \( N_{A} \) segments and a B-block of \( N_{B} \) segments (figure 1),
joined together at one end to give a linear chain with \( N = N_{A} + N_{B} \) total segments and composition fraction \( f_{A} = N_{A}/N \).
Figure 1 - A diblock copolymer with \( N_{A} \) segments in the A-block and \( N_{B} \) segments in the B-block.
The strength of interactions between A and B segments is controlled by the Flory-Huggins parameter, \( \chi \), which is inversely related to temperature (i.e., low \( \chi \) corresponds to high temperature).
When the A-B interactions in a melt of DBCs become sufficiently unfavourable (i.e., \( \chi \) becomes large enough) they microphase-separate, forming periodically ordered structures with domains on the nanometer scale.
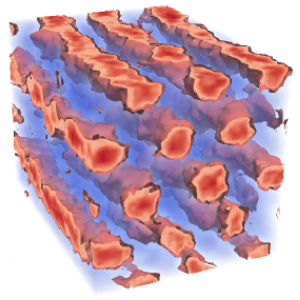
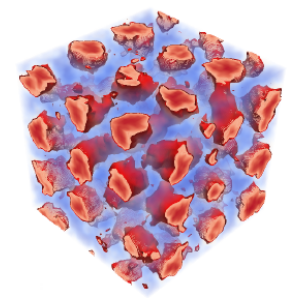
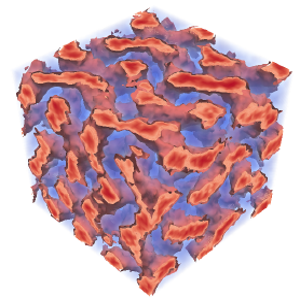
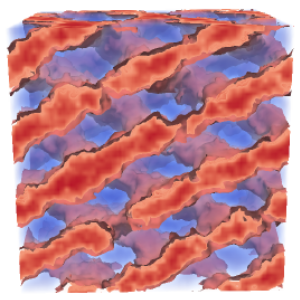
The equilibrium structures include the classical lamellar (L), cylindrical (C) and spherical (S) phases, as well as the complex gyroid (G) and Fddd phases (see figure 2).
Monodisperse vs Polydisperse DBCs
The typical model for studying diblock copolymer phase behaviour is the monodisperse melt, in which the \( n \) molecules of the system
are identical with \(N_{A}\) monomers in the A-block and \(N_{B}\) monomers in the B-block.
However, a melt of monodisperse molecules is difficult, time-consuming and expensive to produce in real experiments.
There are cheaper chemical techniques to manufacture DBCs, but they result in relatively high levels of polydispersity.
In a polydisperse system, the molecules are no longer identical.
There is a distribution of lengths in the A-block, the B-block or both, referred to as a molecular-weight distribution (MWD).
Indeed, experimentally produced diblock copolymers are never truly monodisperse and always have at least a narrow MWD.
The amount of polydispersity is measured by the polydispersity index, \( \mathcal{D} \), which is the ratio of the distribution's
weight-average to number-average molecule length.
For the A-block, this is can be expressed as
\[ \mathcal{D}_{A} = \frac{(N_{A})_{w}}{(N_{A})_{n}} = \frac{\sum\limits_{N_{A}} N_{A}^{2} n_{N_{A}}}{n(N_{A})_{n}^{2}}, \]
where \( n_{N_{A}} \) is the number of molecules in the distribution with an A-block of length \( N_{A} \)
and
\[ (N_{A})_{n} = \frac{1}{n} \sum\limits_{N_{A}} N_{A} n_{N_{A}}, \]
is the number-average molecular weight of the A-block.
The polydispersity index is \( \mathcal{D} = 1 \) for monodisperse molecules and increases as the MWD broadens.
One of the motivations of this project is to determine whether the novel self-assembly properties of diblock copolymers remain with the
introduction of polydispersity, as well as how phase boundaries and properties such as domain size are affected by it.
Self-consistent Field Theory (SCFT)
Imagine looking a single DBC in a melt.
It has complicated interactions with all the other polymers in the system and capturing them all is a difficult mathematical and computational challenge.
SCFT addresses this problem by replacing the interactions that a polymer has with other chains by mean fields.
Monodisperse Phase Diagram
SCFT has been enormously successful in the study of DBCs, producing the famous equilibrium phase diagram for a monodisperse melt shown in figure 3.
It displays the various ordered phases, which are separated from the disordered phase by the order-disorder transition (ODT).
It is also worth noting that the phase diagram is symmetric about \( f_{A} = 1/2 \).
Figure 3 - The self-consistent field theory phase diagram for diblock copolymer melts.
Figure 4 - A schematic representation of the effect of fluctuations on the SCFT phase diagram in figure 3.
Polydisperse Phase Diagrams
In 2007,
Matsen used SCFT to investigate the effects of A-block polydispersity
(monodisperse B-block) on the DBC phase diagram.
The MWD took the form of a Schultz-Zimm distribution, with the probability of a chain having \( N_{A} \) A-segments being
\[ p(N_{A}) = \frac{ k^{k}N_{A}^{k-1} }{ (N_{A})_{n}^{k} \Gamma(k) } \exp \left( - \frac{kN_{A}}{(N_{A})_{n}} \right), \]
where \( k = 1/(\mathcal{D}-1) \) and \( \Gamma(k) \) is the
gamma function
evaluated at \( k \).
Matsen found that in addition to skewing the phase diagram
and inducing areas of macrophase separation (the phase diagrams can be seen in the abstract of the
linked paper), the order-disorder transition (ODT)
gets shifted down to lower values of \( \chi N \) at all compositions (\( f_{A} \)) as polydispersity increases.
This effect is demonstrated schematically in figure 5.
Figure 5 - Schematic representation of how increasing A-block polydispersity shifts the ODT to lower values of \( \chi N \) at all compositions, \( f_{A} \), in SCFT.
Figure 6 - Schematic representation of how increasing A-block polydispersity in experiments shifts the ODT to
lower values of \( \chi N \) at low values of \( f_{A} \), and to higher values at high \( f_{A} \).
Limitations of SCFT
Unfortunately, the mean-field nature of SCFT means that it doesn't include the fluctuation effects that are inherent in real statistical systems.
As a result, we are interested in fluctuation corrections to figure 3, which are controlled by the invariant polymerisation index,
\( \bar{N} = a^{6}\rho_{0}^{2}N \), where \( \rho_{0} \) is the segment density and \( a \) is the statistical segment length.
SCFT corresponds to the case where \( \bar{N} = \infty \), with fluctuations increasing as \( \bar{N} \) is reduced.
The main effects of fluctuations on the monodisperse phase diagram in figure 3 are that the ODT gets shifted upward, and we get direct transitions between the disordered and ordered phases.
For example, there will be a direct transition beween gyroid and disorder as indicated schematically in figure 4.
Experimental Phase Diagrams
Monodisperse Phase Diagram
In 1994,
Bates et. al. performed experiments to produce monodisperse phase diagrams for three different DBC chemistries:
PE-PEP (\( \bar{N}=27 \times 10^{3} \)), PEP-PEE (\( \bar{N}=3.4 \times 10^{3} \)) and PI-PS (\( \bar{N}=1.1 \times 10^{3} \)).
Each of the phase diagrams exhibited the spherical, cylindrical and lamellar phases, but no gyroid or Fddd.
There was, however, a region of another phase known as perforated lamellar in the region where SCFT predicts gyroid.
Indeed, later experiments by
Hajduk et. al. and
Vigild et. al.
showed that perforated lamellar is actually a long-lived metastable state that eventually converts to gyroid.
Even more recent experiments by
Wang et. al. and
Takenaka et. al. have also confirmed the presence of Fddd on both sides of the phase diagram.
Whilst the experiments and SCFT phase diagrams exhibit a lot of good qualitative agreement,
the significant differences are due to the effects of fluctuations near the ODT in the experiments:
the shifting up of the ODT and direct transitions between disorder and the ordered phases.
Polydisperse Phase Diagram
In 2007,
Lynd and Hillmyer studied PEP-PLA and PS-PI diblocks where the
PLA and PS blocks were polydisperse and the other blocks had very narrow molecular-weight distributions.
By fitting their data to a functional form for \( \chi \), the authors presented plots of the degree of segregation at the
ODT, \( (\chi N)_{\textrm{ODT}} \), as a function of polydispersity at several diblock compositions, \( f \).
They observed that for \( f_{\textrm{PLA}} \lesssim 0.6 \), there was a decreasing trend in \( (\chi N)_{\textrm{ODT}} \)
as polydispersity increased, while at slightly larger compositions \( (\chi N)_{\textrm{ODT}} \) increased with polydispersity.
The same trends were observed in the higher molecular-weight PS-PI system, where increasing polydispersity
decreased \( (\chi N)_{\textrm{ODT}} \) for \( f_{\textrm{PS}} \lesssim 0.51 \), but led to an increasing trend
for \( f_{\textrm{PS}} = 0.64 \).
Hence, in a diblock copolymer system where one block is polydisperse, the experiments broadly observe that increasing
polydispersity in the minority block leads to a decrease in \( (\chi N)_{\textrm{ODT}} \), which is in qualitative
agreement with the SCFT predictions.
However, increasing polydispersity in the majority block increases \( (\chi N)_{\textrm{ODT}} \), the opposite of the
downward shift predicted by SCFT. In a further departure from mean-field behaviour, experiments have only observed
direct transitions between between disorder and the non-spherical ordered phases.
As was the case in the monodisperse system, the significant differences between the predictions of SCFT and experiments
in the vicinity of the ODT are suspected to be due to fluctuations. It is therefore of interest to confirm whether this
is the case with simulations.